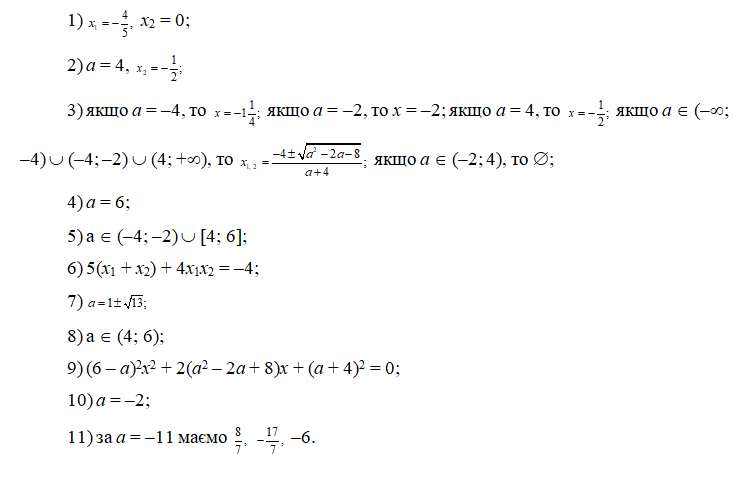Для проведення практичної, самостійної або тематичної контрольної роботи з теми «Квадратні рівняння з параметрами» у дев’ятому класі з поглибленим вивченням математики або у дев’ятому класі, що працює за звичайною програмою, але має високий рівень знань, можна використовувати комплексні задачі. Під комплексною задачею з цієї теми розуміємо, наприклад, задачу, яка містить квадратне рівняння з параметрами і різноманітні завдання, пов’язані з ним.
Розв’язання комплексних задач допомагає учням:
- закріпити вміння та навички дослідження існування розв’язків та їхнє знаходження;
- визначити знаки коренів та правильно їх розташувати відносно одного або двох чисел залежно від числових значень параметра;
- розв’язувати інші вправи;
- зрозуміти роль теореми Вієта у подібних задачах;
- виробити навички обчислювального характеру, вміння аналізувати, досліджувати і робити висновки;
- сформувати ширше уявлення про рівняння такого класу.
Пропонуємо шість варіантів таких задач, приблизно однакової складності і розрахованих на два уроки. Перший варіант подаємо з розв’язанням, а до інших варіантів — відповіді.
Завдання досить легко диференціювати за рівнями:
- початковому і середньому рівням навчальних досягнень учнів відповідають завдання з номерами 1—3;
- достатньому рівню — 4—6;
- високому рівню — 7—11.
Вчитель, зважаючи на рівень підготовленості класу, може на свій розсуд спростити чи ускладнити деякі завдання, збільшити або зменшити їхню кількість у роботі.
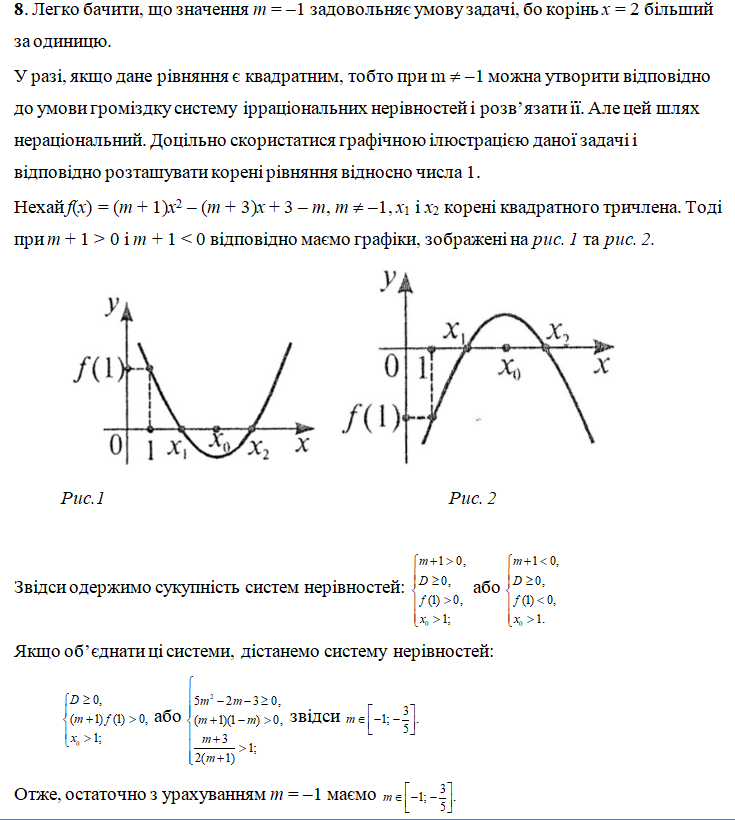
Завдання 1
Маємо рівняння: (m + 1)x2 – (m + 3)x + 3 – m = 0, m є R.
Завдання 6
Дано рівняння: (m – 1)x2 + 2(m – 3)x + m2 – 9 = 0, а є R.
Автор: Володимир Сучков,
учитель математики, методист СШ № 271 з поглибленим вивченням інформаційних технологій, м. Київ
Використані джерела
Навчальні програми з математики URL: https://mon.gov.ua/ua/osvita/zagalna-serednya-osvita/navchalni-programi/navchalni-programi-5-9-klas (дата звернення: 15.05.2019 р.)